This is the homework that follows out discussions of drag forces and periodic driving forces. Most of these problems are really about getting the differential equation for simple harmonic motion (no damping or driving) but it takes time to develop a level of comfort with this material so I didn't through it at you last week. Remember that you have a blueprint for how to approach these problems that I handed out in class or you get access it here.
1) Show that the oscillation frequency for a mass attached to two identical springs in series is given by
2) Repeat problem 1) but with two different spring constants, k1 and k2, and determine the new expresion for the frequency.
3) Repeat problem 1) but now place the springs in parallel with different spring constants, k1 and k2, and determine the new expresion for the frequency.
4) Based on your results from the previous problems create a model for the effective or apparent spring constant for two springs in parallel or in series. Said another way, what is the spring constant of a single ideal spring that would behave the same in either of these settings? You will have one expression for springs in series and a different one for springs in parallel.
5) If you've watched the video of the MIT Opencourseware version of PH213 you will have noticed the demo of the floating tube (vertical) which bobs up and down in a tank of water in a pleasing fashion. Assume the cylinder is uniform in cross section, has diameter d, is L long, and floats with a length u underwater. At t=0 you push it an additional distance z underwater and release it. You will need to "know", after you complete your freebody diagram, that the bouyant force is equal to the weight of the water displaced by the cylinder. What is the frequency of oscillation if you are using physics grade distilled water? Will the frequency of oscillation increase or decrease in salt water? Explain your reasoning.
[(1/2π )(g/u).5, no diff]
6) We discussed lightly the effects of a drag term on the differential equation for simple harmonic motion. Given the differential equation for a damped harmonic oscillator below show that the proposed (guessed) solution actually works and satisfies the equation. This is another example where I am asking you to use a trial function with a number of undetermined constants. When you 'put the trial solution into the diff eq' you will find (algebraically) that things can only be true if the constants have particular values (see b and ω below). You will find that there are no constraints on C (the amplitude) or φ, the phase shift.
![]()
![]()
![]()
7) The following plot shows an object experiencing damped periodic motion. Assume that the vertical axis is labelled in m. Estimate the maximum velocity at each succesive point where the curve passes through the equilibrium point. Use the tools we have developed for well behaved periodic motion. You should be able to get 5 data points off the plot. For each one determine the kinetic energy of the 100g mass which this plot represents. (do so!). Is the loss of kinetic energy constant from point to point? Can you tell if the rate of change of the kinetic energy is a constant percentage of the previous data point?
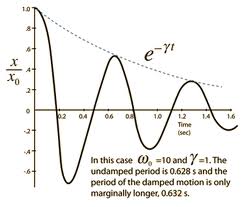
8) If I "pump" this mass by adding 0.5 J of energy to each cycle what will happen? There are, as usual, several ways you can think about this. If I start pumping from the very begining what will happen? If I start pumping the system after 4 seconds what will happen? What would happen if there were no damping in the system while I was pumping it. These are qualitative questions that test your understanding of question 7).
