The fundamental point of this homework set is for you to experience some to the basic tasks that come up again and again in settings where differential equations describe some physics of engineering process. These include checking that a solution works, applying initial conditions to determine constants, applying boundary conditions, and figuring out units/dimensions. A common experience in our society that is actually described by a differential equation is a loan. Here is a pdf summarizing the explorations that I have typically done. We may or may not have done this explicitly in class so read the document.

1) Imagine that you hoped to get a 30 year loan at 5% annual interest (fixed) compounded monthly with an initial value of $200k. How much principle do you have left to pay after the 20th year of payments?

2) Let's approach this a slightly different way. If you think you can afford $1100.00/month in payments on your loan (not counting taxes and insurance costs) how much can you borrow at 4% annual interest (fixed) on a 20 year loan?

3) If the capital equipment you need to buy for your production facility costs $40k and you can get a 10 year commercial loan at a fixed rate of 8% what are your monthly payments going to be?

4) The following differential equation is called the logistic equation and it describes a population that has a death rate that depends on how big the population is (crowded).

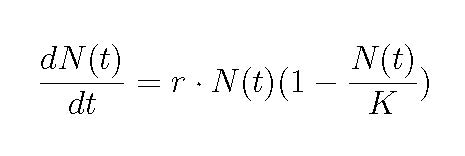
What are the units for each term and constant in this expression?

5) The solution to this logistic equation is purported to be....

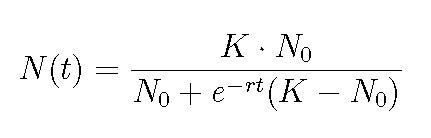
Show that this solution does indeed work (if it does) or fail (how?). Think of this as a trial solution and use it like we did with the trial solution in our class explorations.

6) What does this solution say about the population of whatever this creature is at t=0 and "after a long time"? Look at the solution first and then think what the differential equation has to say......does this make sense in the physical world?