Purpose:
To explore the relationship between what we calculate/analyze in an academic setting and what that looks like in the wild where the resistors and capacitors are not some Purdue like object but rather free range devices with a mind of their own.
We analyzed the following circuit when the impedance of the capacitor was much less than, equal to, and much greater than the impedance of the resistor.
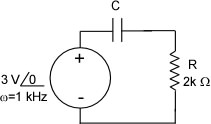
Procedure:
1) Wire the illustrated circuit on a small project board. We will use the function generator as the power supply. A capacitor will be provided which you will eventually change. Be careful to define a clear ground point in your circuit layout as well as where you will connect the function generator. After having the circuit verified by the instructor you may set up the function generator and begin your measurements.
Several things to note about the set up. It is very handy to be able to see the voltage source on one of the oscilloscope channels as a constant reference. This allows you to monitor the amplitude, phase, and frequency. To do this you can attached the BNC T connector to the function generator and run one BNC cable to the scope and one to the circuit. Given the physical set up of our digital scopes it might make sense to use channel 2 for this to keep the cables out of the way. Select the frequency for the function generator that you determined makes the impedance of the capacitor equal to that of the resistors.
At this point you can verify that your AC source has the appropriate amplitude and DC offset (no offset in today's lab) BEFORE you connect it to your circuit. Note: If you have connected the function generator to channel 2 on the scope you will need to select CH2 as your trigger source on the scope control panel. The BNC to clip connector allows you to easily connect the second output of the T to your circuit as indicated. The red clip lead is (+) by convention and the black is (-). You may find that when you attach the function generator to the circuit that it seems to change. If this is significant (it wasn't for me) then the implication is that your circuit is overstressing the internal electronics of the function generator. Stop and check everything and get input from your lab instructor before proceeding if this happens.
2) Set up your function generator to provide a 3 V peak to peak sine/cosine function at an ω of 6 kHz. Use the oscilloscope to verify this set up. Now you can observe the voltage across the resistor (vR) at the same time that you observe the voltage provided by the function generator (vS). This will require the use of both input channels on the oscilloscope. Measure the amplitude of the voltage across the resistor and any phase shift relative to vS. Once this is completed repeat the same measurements at a low frequency (f around 20 Hz) and a high frequency (f around 1 MHz). You should observe that at one of these frequencies vR is quite small and at the other end vR has the same amplitude as vS. At one end of the spectrum you should observe a phase shift of essentially 0 and at the other π/2. If you don't observe these general features be sure to talk to the lab instructor about what is happening (you may need a different capacitor).
As we have discussed in the classroom portion of the course the impedance of the capacitor is dependent on the frequency. At some frequencies the impendance of the capacitor dominates the circuit at at other frequencies the resistor dominates. How does this show up in your measurements for this part?
You are also learning to use your oscilloscope in new ways in this lab. You are using both inputs and comparing the phase of the different signals. I expect that you will actually calculate the phase difference in degrees to be sure you understand how this process works. You will likely find that you need to adjust the scales on the resistor channel often in this process as well as the trigger levels. Remember that the silly scope will apparently show you a signal even though it was from a while ago.
3) Having explored how to make phase and amplitude measurements we now need to explore how to share this data. We will be using semi-log plots to do so since the voltage and phase are only changing a little (the linear vertical scale) while the frequency is changing 5 orders of magnitude hence the log scale. What we are really plotting along the horizontal axis is the log of the frequency but the semi-log paper makes this easier for us. For this section of the lab you will fill in the plot of vR (on the vertical linear axis) and phase (also along the vertical axis) vrs frequency (on the horizontal log axis). One of your tasks will be to figure out which way the paper should go since there are two choices. Take enough data to make the shape of the curves clear. In your lab notebook note what the relationship between these curves appears to be.
4) At some point in this process you should do a formal mathematical analysis of the 'circuit' and that indicates the amplitude and the phase of vR. This will be slightly complex because you don't know the value of C at this point. Determine what value of C leads to a phase shift of π/4. From your plot in the previous step you should be able to find the frequency at which the phase shift is close to π/4. From this information calculate the value of the capacitor in your circuit.
5) Repeat steps 2 and 3 using capacitors 10 times larger and smaller than the one you originally used. Determine and sketch the amplitude and phase relationships that you observe in these two cases. This data should be plotted on the same graph paper as the previous one so you can see and understand the relationship between the plots. Be sure to indicate which plot is the big capacitor and which is the small one. You do NOT need to repeat step 4 unless you wish to.
Lab "Notebook":
The following information should be clearly presented in your lab "notebook" along with explanatory and insightful commentary.
I) A clear drawing of the circuit constructed including the connections to the function generator and oscilloscope.
II) Show how you calculated/determined the value of the capacitance that matched the impedance of the resistor (π/4 phase shift).
III) Representative plot(s) of the output signals (voltage and phase) observed at various points in the process for all the capacitors you examines.
IV) Think about and articulate your understanding of the difference between a capacitive load and a resistive load in the context of this lab. Explain conceptually why the plots look the way they do and why larger capacitance has the effect that it does. Be sure your discussion explains the phase shift as well.
V) Predict what you would expect the plot of the voltage and phase across the resistor if the capacitor is replaced by an inductor. Explain your reasoning.
