Mood Brightener: ...more from Stay Homas. (Confination VII)
Your Conceptual Goals for this section: Electric Potential (ΔV)
Falstad Math/Physics Simulations:
This is the qualitative portion of our discussion about Electric Potential:
Connection back to Work/Energy:
You should be duly suspicious that any description that has potential in it's name will have something to do with energy. What we found in PH211 (Newtonian Physics) was that understanding energy gave us a different way to look at problems. Energy methods offered different insights and sometimes helped simplify and clarify our understanding.
The core physics concept was that forces on objects that move energy (which is formally called 'doing work'). When we consider the work done by the net force acting on an object we get the Work/Energy theorem:
If we then consider individual forces we learned that the energy moved by a particular force was given by:
....remembering that the dot product is a particular form of vector 'multiplication'. We calculate this by noting the the dot product introduces the cosine of the angle between the force vector (F) and the displacement vector (Δ x).
Any charge which is in an E field experiences forces and when the charge moves or is moved then work is done (energy is moved!).
The last connection to keep track of is the relationship between the change is some potential, or stored, energy and the work done by a force. Remember that the difference between work done and the change in potential energy have the same magnitude but different signs because energy taken away from an object (-) ends up adding to (+) a stored energy reservoir somewhere. Formally we describe this as:
-WAB = ΔPEAB
In words this says the work done by a particular force as an object moves from A -> B is the opposite sign, but same magnitude, as the change in the potential energy stored as the object moves from A -> B. What do you expect to happen as the object moves from B -> A with the same force?
Caveat: Only forces where WAB does NOT depend on the path (how you travelled from A -> B) can be described with potential energy.
Energy Tool(s): Our primary tool for approaching problems where energy is a factor is the energy bar charts. If you need a rough review see the discussion in the Work/Energy Breadcrumbs from last term. Bar charts are a general tool for physics quantities that are conserved. This includes energy as well as momentum and some other concepts we haven't discussed.
Gravitational Potential Differences (operational definition):
Remember how we determined the gravitational potential energy? We figured out the work done by the force of gravity as a mass is moved from point A to point B. There may well be other forces doing work as well but we were only focused on the force of gravity.
Here's the thing we didn't do with gravity. What would happen if instead of calculating the total energy stored by gravity we calculated the energy stored per unit of mass (kg)? Calculate the change in graviational potential energy when I move a 2 kg, 3.5 kg, and 53 kg object on top of a 1.3 m high counter? Now calculate the energy per kg in each case. What you have done is:
something = Wforce of gravity/m = constant? (what are the units?)
gh = W
Fg /m = gh where the units are: m2/s2 or J/kg!!
The fact that this number is constant for that table top regardless of mass is of interest. It's not energy exactly but it is closely related to energy. Eventually we came to call this the gravitational potential difference between the two points. Notice how the use of language invites confusion. If I tell you that two points have a gravitational potential difference of 34 m2/s2 can you tell me if they are further apart than the 1.3 m of the counter? How much energy does it take to put 1 kg up on this new location?
Notice that the change in gravitational potential is NOT the same as the change in gravitational potential energy!!!
Electrical Potential Energy (EPE):
The first thing we have to do is convince ourselves that if I figure out the work needed to move a charge from A -> B that there are many paths by which I can do that and still get the same number. This is a characteristic that is needed to be able to define a potential energy. Sketch a uniform E field, you pick the intensity, pointing in some direction. Pick two points A and B in that E field. Put a charge, you pick the sign and magnitude of the charge, at Point A. Calculate the force (direction and magnitude) on the charge. Draw a path from A to B where the first leg is perpendicular to the E field and the second is parallel to the E field and calculate the work done by FE on each leg (one of them should be 0, why?) Can you find other paths where the work done by FE is the same? Many other paths?
This means there is a well behaved electric potential energy like that for gravity.
Electrical Potential Difference:
Now calculate the change in the electric potential (this is completely analogous to what we just did with gravity).
What are the units of this quantity? Is it energy? Is it related to energy?
So what does physics typically do when it has a new concept and a new set of units? It gives them a new name of course? J/C we call Volts and the change in the electric potential we label ΔVAB (it's nice that the label and the units match eh?)
ΔVAB= WAB/q
Because WAB is a scalar and not a vector that means ΔVAB is also a scalar and NOT a vector. This is important when we get to problems with multiple charges and distributions of charges. Do you notice that this means that the change in the electric potential energy is given by
-ΔPEE= qΔVAB= WAB
In our energy bar charts we often label this as qΔV potential energy.
Energy Bar Charts:
If we consider our most general form of the energy bar chart from PH211 (Energy Bar Charts are discussed here and here for PH211) shown below....
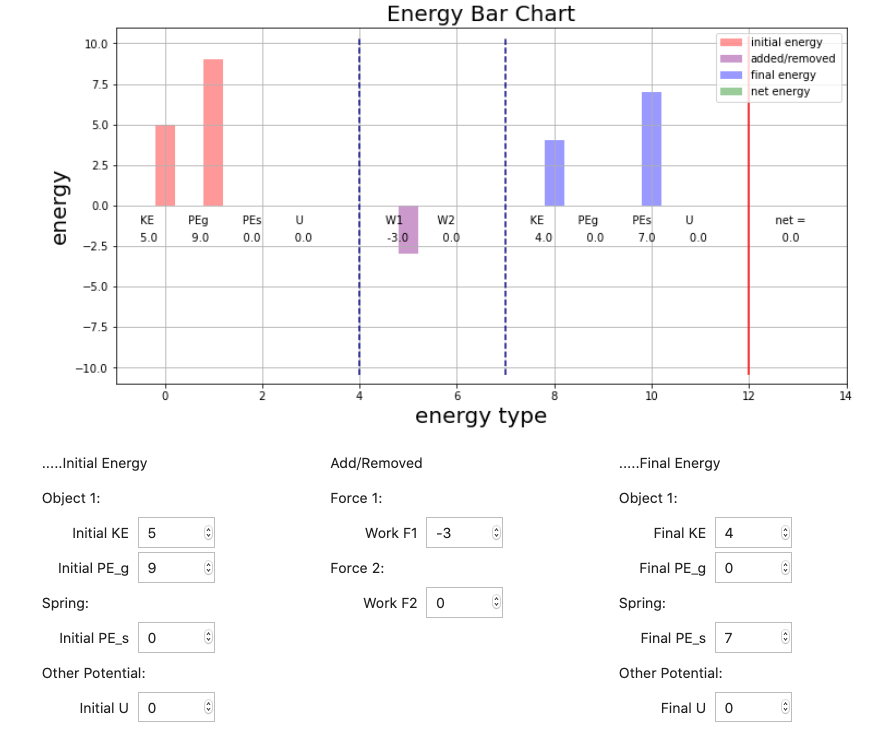
On the left and right of the bar chart there is an unassigned column labeled U which you may remember was set aside for some future source of potential energy. Well here it is! ΔPEE= qΔVAB (give or take a minus sign. Like h in the gravitational potential energy expression you can pick a convenient location where h = 0. Only Δh actually matters in an energy sense. The same thing is true for the electric potential (voltage). As long as you know the voltage difference between the points of interest you can pick any point to be V = 0 V.
NOTE!! There is an important difference for qΔVAB energy because we have both (+) and (-) charges. You will need to determine conceptually whether energy is being taken from the charge and 'stored' as potential energy or given to the charge and 'removed' from the bank of potential energy. When a (+) charge moves up in potential energy is being taken from the charge and stored as potential energy just like a cannon ball going up hill. On the other hand a (-) charge moves to a higher potential (ostensibly 'uphill') and it gains energy by drawing energy from stored potential energy. Same voltage hill but very different effects. Be careful!
Connection to E Field:
We define the electric potential V in terms of the work done WAB. But work depends on forces as in WAB = F . Δx and F is connected to the E field as we found last week (F = q E). Putting that all together in the context of a uniform E field where the force on the charge would be constant we get the following relationship.
ΔVAB = WAB/q = [F Δx]/q = [qE] Δx/q = E Δx
We will explore this connect more in a few days but for those who are wondering about it here it is.
Assignment Breadcrumb Reading: Bb Test
Potential:
The electric potential is defined to be the work done by the E field as a charge moves between two points divided by the magnitude of the charge moved (V = WAB/qmoved). There is an equivalent quantity called the gravitational potential (not potential energy!) which is defined similarly. What is the gravitational potential of a 4 kg mass on a 2 m high counter and what are it's units? Hint: In the end the 4 kg doesn't matter.
Before Next Class:
Assignment HW: Bb Test
Basic Practice: Electric Potential
If it takes 25 mJ of work to move a 500 nC charge from A to B what is the electric potential difference between A and B?
Assignment HW: Bb Test
Energy Bar Chart:
The plot shows the electric potential along a line in space. ? A proton traveling in the +x direction at x = 0 and is brought to a stop at x=3 mm. What was the kinetic energy of the proton at x=0? Think in terms of energy from PH211 and remember that the energy moved by the E field is qΔVAB . You may find it helpful to think in terms of the energy bar charts we used in PH211 (see link above).
Looking Ahead:
Look ahead to the next Breadcrumb: Electric Potential II
Assignment Breadcrumb Reading: Bb Test
Potential: Axis of Dipole
A dipole whose charges are +1.2 mC and -1.2 mC and are separated by a distance of 62 cm. What is the Electric Potential 62 cm past (further away from the center) either charge.Be sure to know the difference between the point nearest the (+) charge and the point nearest the (-) charge.
